Evaluating seven squared and 17 squared gives ππ squared is equal to 49 plus 289. Now, we have an equation that we can solve in order to find the length of ππ. In this triangle, this means that ππ squared is equal to seven squared plus 17 squared. Remember the Pythagorean theorem tells us that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the two shorter sides.
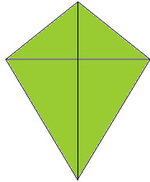
As the triangle is right angled, we can apply the Pythagorean theorem. And weβd like to calculate the length of the third side ππ. In this triangle, we know the length of two of the sides: they are seven and 17. If we focus on the lower part of the diagram, we can now see that the line ππ is part of a right-angled triangle - triangle πππ. And hence, all four of the angles where they intersect are right angles. This means that the lines ππ and ππ are perpendicular. One of the key properties of a kite is that its diagonals are perpendicular. The length weβve been asked to find is ππ, one of the longest sides of the kite.
Weβve been given the length of two lines in the diagram: ππ and ππ, which are the diagonals of the kite, as each connect a pair of opposite vertices. In this question, it means that ππ and ππ are the same length and ππ and ππ are the same length. What does this mean? Well, a kite is a quadrilateral with two pairs of consecutive congruent sides. Weβre told that the quadrilateral ππππ is a kite.
0 kommentar(er)
